An Example of Advanced Counting
(or, Details Matter)
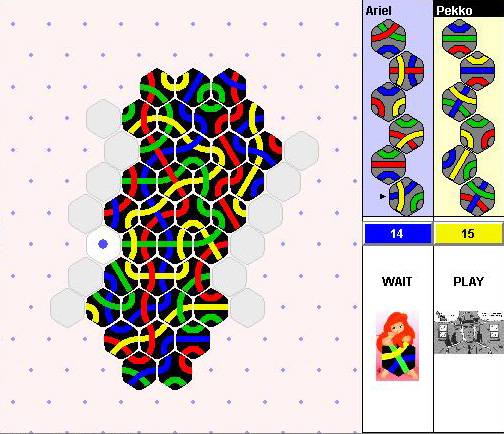
Consider this position, taken from game
M!Ariel-Pekko-2002-04-11-0300
 These are my hints for Playing Tantrix
online
These are my hints for Playing Tantrix
online
An Example of Advanced Counting
(or, Details Matter)
Consider this position, taken from game
M!Ariel-Pekko-2002-04-11-0300

The quick evaluation of this position is pretty
straightforward;
the position is close, but the crucial play is to prevent Blue from
connecting
her main line with the secondary line, probably by blocking the top
side.
Making a blocking move is also the obvious choice because there are no
connecting or extending moves immediately available. But
which one?
Several tiles make immediate blocks. The tiles available to
block
give either a YYR or a YYG, either with two candicate tiles remaining.
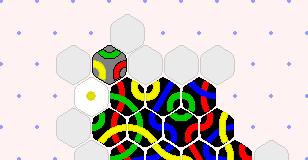
There are two YYR tilkes remaining. This looks superficially better for Yellow, because Yellow gets to play an additional tile. Other things being equal, this is better than the alternative at the right. |
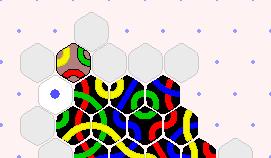
There are two YYG tiles remaining. This looks superficially worse for Yellow, becuase blue gets to play an additional tile. Other things being equal, this is worse for Yellow than the alternative at the right. |
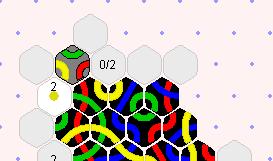
No Tiles can be played until endgame! And even better, if any of those tiles remain when endgame starts, they will permanantly block blue's line. |
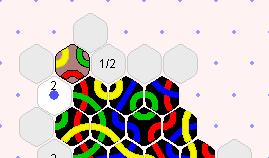
One tile can unblock before endgame. |
So in this case, the general concept of pair blocking pays off bigtime! But you can't know unless you count. Depending on the exact tiles remaining, two blocking tiles that appear to be a tossup can be hugely different in actual effect - it all depends on what information you bring to bear on the problem.