An Eye Shape library for Computer Go

The shape library is available as a Java applet that you can play against, and generally use to study tsumego.

When solving life-and-death problems, one of the hardest things for a computer to determine is when to stop a search. Benson's proof describes the circumstances where groups are unconditionally safe, but a practical problem solver should stop much sooner: when a group is safe assuming best play. Safety heuristics can be pretty reliable if the number of liberties is large enough and the position is simple enough, but it is useful to have a library of solved positions to bridge the gap between the absolute safety described by Benson's algorithm and the highly probable safety for groups with lots of liberties. This article describes some aspects of such a library.

There are only 164 distinct "eye shapes" up to size 7 (533 up to size 8), but we must also consider the orientation and location of the shape, the connectivity of the stones surrounding it, the number of outside liberties, the player to make the first move, and the status of the stones that would be the capturing stones if the shape is dead. Many small scale life-and-death problems involve KOs, and a few shapes can be played either for a Ko or for a Seki. In these situations, the status of a particular shape can't be considered in isolation from the global situation. When all these factors are considered, the number of distinct positions, with possibly different solutions, is very large.

Figure 1

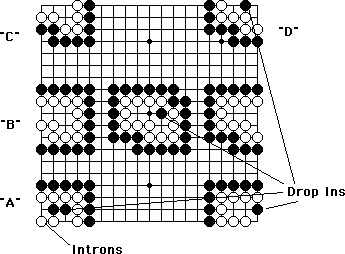
If you'd rather see an ascii representation, go Here

Figure 1 shows the "bent four" shape placed in a variety of positions.

At "A", the shape is positioned such that there are two distinct groups surrounding the shape; The inside group is called an "intron" group. In many of the more complex situations, the intron groups can be captured in the process of a fight for life.
The surrounding stones can have outside liberties, as at "B" The outcome of many positions is sensitive to the number of outside liberties. Frequently, the progression is similar to "dead" with 1 liberty; "seki" with 2 liberties; "alive" with 3 liberties.
Sometimes, the stones surrounding the shape are not simply connected, as occurs at "C". In these cases, the information in the shape library is not directly usable to detemine life or death of the surrounding group, but can still be used under some circumstances.
Opposite-colored "drop in" stones can be inside the shape, for example the black stones at "D".

Accordingly, the library contains life-and-death information for the following combinations:

    164   shapes (plus a few auxiliary shapes)
  x   9   different positions on the board
  x 2^n   different patterns of "dropped in" 
          stones of the opponent's color
  x   2   (moving first or second)
  x  ~3   0-2 outside liberties, plus more for some shapes

  for a total of 560,523 Solved positions in the library

Some interesting numbers

of 560,523 solved positions in the library

62,003 (11%) are irrelevant, impossible or unreachable positions.
498,220 (89%) are reachable positions
375,986 (57%) are terminal (no possible utility in moving for either player)
107,528 (28%) are not completely determined; sente (plus ko threats) determines the outcome. Most of these positions occur in the corners.
15,605 (4%) are not killable (absolutely alive)

For each of these 560k positions, I store the outcome and the move that leads there. This allows me to reconstruct the game tree (assuming best play) from any position found in the library, and to make tactical decisions about the best course of play (ie; to continue to fight or to give up) without performing a search.

Construction and Representation notes:

My program builds its library of shapes by brute force, one generation at a time, starting with a single stone and adding additional stones in all possible ways. While building the set of shapes, it detects equivalent isomers by generating all 8 isomers of each new shape and comparing them to all previously generated shapes.

Once the complete set of shapes is generated, the program builds a discrimination network of simple tests that can rapidly recognize any of the shapes any orientation or permutation in any position on the board. Using a hashing algorithm based on ideas of Zorbrist citation)

sidelight for programmer-weenies Originally, I used an extremely clever bit of lisp code that generated a discrimination network, consisting of a preliminry hash plus an automatically generated function for each hash collision. Zorbrist' hash algorithm blew it all away (I found it 25 years late!) and incidentally made it simpler and faster.

Taken together, this provides most of the machinery needed to recognise a shape "on the board" and locate the applicable entry in the shape database.

The database was generated by searching, using the same problem solver which now uses the database as a shortcut. The original search which built the database ran for weeks. The resulting database occupies approximately 1.5 megabytes. At first, a significant number of errors existed, mainly due to bugs in the problem solver, and due to the fact that any errors were immediately used to generate other bogus "solutions". However, since about 1987 (I've been at this a long time!) the shape library has been completely stable.

Since June 1994, I have had the opportunity to test my problem solver (and therefore the underlying shape library) against a thousands of Tsumego problems provided by Thomas Wolf (T.Wolf@qmw.ac.uk) and have had to make exactly 3 minor corrections. I consider this to be a pretty solid demonstration of the fundamental soundness of the library.

How to use the shape library:

In the following discussion, "the shape" means the eye shape itself, "the surrounding stones" means the stones which surround the eye shape, and "the capturing stones" means the oppose-colored stones that surround the capturing stones.

The raw information in the shape library can only be used when the external conditions assumed by the library are actually present. In addition to recognizing the shape and characterizing its position on the board, we also need to know the connectivity and liberty count of the surrounding stones, and must have a reliable estimate the status of the capturing stones.

If the capturing stones form an impenetrable wall, and there is no room to make additional eye shapes, and the the library says the existing eye shape is dead, then searches can be terminated immediately, even if the connectivity of the surrounding stones is imperfect. If the surrounding stones could be connect as expected by the library, the shape would still be dead.
If the database says a shape is alive, and the surrounding stones are simply connected, then searches can be terminated without regard to the status of the capturing stones.
When the eye shape is dead (ie;forms only one eye) the move tree stored in the database can be used to guide the formation of that eye shape, so only one alternative need be considered. If the surrounding stones do not have the required connectivity, then the other possibilities have to be considered too, but the library move can be tried first. This kind of advice is not as good as terminating the search entirely, but it is still a bug help in reducing the number of positions that have to be examined.
Using the above techniques in life-and-death searches typically results in about a 50% reduction in the amount of work required.

Ascii figures

Provided for the poor unfortunates who don't have a graphical interface. Also, not incidentally, relics from when I originally wrote this.

figure 1



        "C"                          "D"
    - - - - - - - - - - - - - - - - - - - - -
    |       o x                   x o   x   |
    | o o   o x                   x o o o   |
    | x x o o x                   x x x o o |
    |   x x x x                       x x x |
    |                                       |
    |                                       |
    |                                       |
    | x x x x x   x x x x x x     x x x x x |
    | o o o o x   x o o o o x x   x o o o o |
    |       o x   x o     x o x   x o       |
    | o o   o x   x o o o   o x   x o o o   |
 "B"|   o o o x   x x x o o o x   x x x o o |
    | x x x x x       x x x x x       x x x |
    |                                       |
    |                                       |
    | x x x x x                   x x x x x |
    | o o o o x                   x o o o o |
    |   x x o x                   x o     x |
 "A"| o o   o x                   x o o o   |
    - - - - - - - - - - - - - - - - - - - - -

Go Back

comments/suggestions to: ddyer@real-me.net

Back to my home page